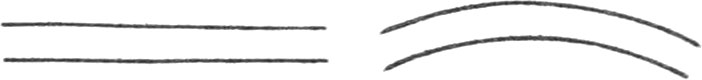A point is that which hath no Parts, and consequently is indivisible.
Definitions necessary for understanding this Treatise.
A Line is Length without Breadth, whose Original is from a Point.
There are three kinds of Lines; viz. Right Lines, Curve Lines, and Mixed Lines.
A Curve Line is that which doth not go directly from one of its Extremes to the other, but winds about.
A Mixed Line is that which hath one Part strait, and the other crooked.
Lines compared as to their Positions or Situations, are either parallel, perpendicular, or oblique.
Parallel Lines are such that always keep the same Distance to each other, and which, if both ways infinitely produced, will never meet, whether they be Right Lines, or Curves.
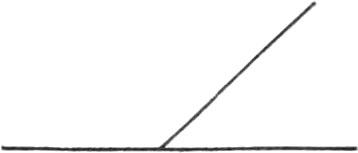
Perpendicular Lines are those that meeting, incline no more to one fide than to the other; and therefore they make two equal Angles, which consequently will be Right Angles.
Oblique Lines are those, which meeting one another, form oblique and unequal Angles, that is, acute and obtuse Angles.
Moreover, Lines have other Denominations; which are as follow:
An upright, plumb, or vertical Line, is that which, if produced, would pass through the Center of the Earth, as the String of a suspended Plummet.
A horizontal Line, or Line of apparent Level, is a right Line that touches the Surface of the Earth in one Point, or which is parallel to a Tangent in that Point.
A Line of true Level is that, whose Points are all equally distant from the Center of the Earth, as the Circumference of the same.
A finite Line is that whose Length is determined.
There are also occult Lines, drawn with the Points of Compasses, or more properly with a Pencil, because then they may be easier rubbed out: These Lines must not be seen when the Work is finished, unless they are left to mow how the Operation is performed; and then they are dotted, which is done with a Dotting-Wheel.
The Lines that must remain, and which are called apparent Lines, are drawn with Ink, put into a drawing Pen, as plain and small as possible, by means of the Screw belonging to it.
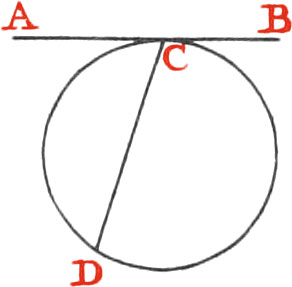
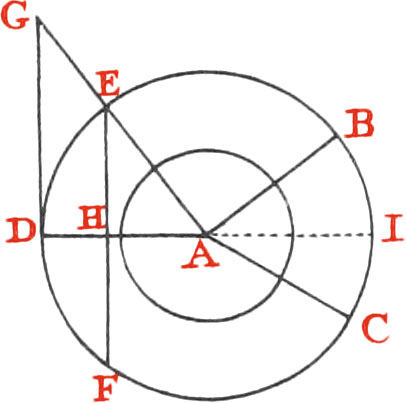
A Tangent is a Line touching a Figure, and not cutting it; as the Line AB.
A Subtense, or chord Line, is that which joins the Extremes of an Arc; as the Line CD.
The different kinds of Curve Lines are infinite; but the simplest, most regular, and easiest to draw, is a Circle.
A circular Line, or the Circumference of a Circle, is a Curve; all the Parts of which are equally distant from one Point in the middle of it, which is called the Center of the Circle.
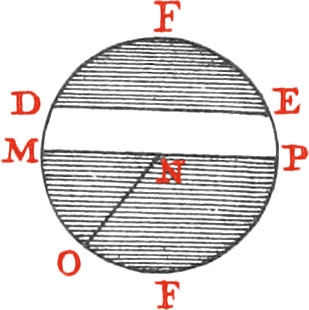
Right Lines, drawn from the Center of a Circle to the Circumference, are called Radii, or Semidiameters; as NO.
Those Chords that pass through the Center of a Circle, are called Diameters; as MP.
The Circumference of every Circle is supposed to be divided into 360 equal Parts, called Degrees.
The Number 360 was chosen by Geometricians for the Division of a Circle, because it may be more exactly subdivided into many equal Parts, without any Remainder, than any other:1 as for example; half of 360 is 180, \(\frac{1}{3}\) is 120, \(\frac{1}{4}\) is 90, \(\frac{1}{5}\) is 72, \(\frac{1}{6}\) is 60, and so of other of its aliquot Parts.
Every Degree is divided into 60 equal Parts, called Minutes, every Minute into 60 Seconds, and every Second into 60 Thirds, &c. which are thus distinguished 40° 3.5′ 49″ 57‴ signify forty Degrees, thirty-five Minutes, forty-nine Seconds, and fifty-seven Thirds. The aforesaid Division serves for measuring of Angles; but the Sub-Divisions into Seconds and Thirds are not used, unless in great Circumferences. The Opening of two different Lines cutting one another, or meeting in the same Point, is called an Angle.
When two Lines cut, or meet each other in one Point on a Plane, the Angle they make with each other, is called a plane-Angle, or a plain-Angle.
When the Lines that make a plain-Angle, are strait Lines, the Angle is called a Right-lined Angle.
If the two Lines forming an Angle, are Curves, the Angle is called a Curve-lined Angle.
If one of the Lines is a Curve, and the other a strait Line, the Angle is called a Mixed- lined Angle.
The two Lines that make an Angle, are called its Sides; the Point wherein they cut or meet each other, being the Vertex.
When an Angle is expressed by three Letters, that in the middle represents the Angle, and the other two the Sides.
In producing or lessening the Sides of an Angle, the Quantity of the said Angle is not at all altered thereby; for the Magnitude of an Angle is not measured by the Magnitude of its Sides.
The Measure of a Right-lined Angle is the Portion of a Circle comprehended between its Sides, whose Vertex is the Center of the Circle: It matters not how big the Radius of the Circle be; because whether the circular Arcs, comprehended between the Sides AB, AC, of the Angle be bigger or lesser, they still have the same Number of Degrees.
If, for example, the Arc of a small Circle be 60 Degrees, which is the sixth part of the whole Circumference, the Arc of a greater Circle will likewise be 60 Degrees, or the sixth part of the Circumference of the greater Circle, and the Angle BAC will be 60 Degrees.
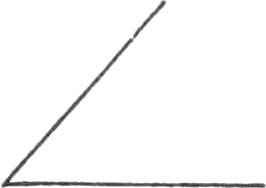
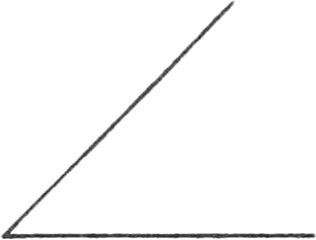
Every Angle is either a right, acute, or obtuse Angle.
The Measure of a right Angle is an Arc of 90 Degrees, which is l of the Circumference of a Circle.
An acute Angle is lesser than 90 Degrees.
An obtuse Angle is more than 90 Degrees.
There can be no Angle of 180 Degrees, which is the Semi-Circumference of a Circle; for two right Lines so posited, cannot cut, but will meet each other directly, and consequently will make but one right Line, which will be the Diameter of a Circle.
The Sine of an Angle or Arc, is half the Chord of double the same Arc: as for example, to have the Sine of the Angle DAE, or of the Arc D E (which is the Measure of it) by doubling the Arc ED, you will have the Arc EDF, whose Chord is EF, whereof EH, its half, is the right Sine of the Angle DAE: the Line DG is the Tangent of the same Angle, and the Line AG is its Secant.
Two Arcs together making a whole Circle, have the same Chord; for it is manifest, that the Line EF is as well the Chord of the greater Arc EBCF, as of the lesser one EDF.
For the same reason two Arcs, which together make a Semicircle, have but one right Sine; as the Line EH is as well the Sine of the obtuse Angle EAI, or of the Arc EBI, which is its Measure, as of the acute Angle EAD, or of the Arc ED. The same may be said of Tangents and Secants.
The Sine of 90 Degrees, which is the Radius or Semidiameter, as DA, is called the Sinus Totus.
A Surface, or Superficies, is that which hath only Length and Breadth.
There are two kinds of Surfaces, viz. Plane and Curve.
A Plane Surface is that to which a right Line may be applied all manner of ways; as the Top of a very smooth Table.
A Curve Surface is that to which a right Line cannot be applied all manner of ways; they are either Convex, or Concave; as the Outside of a Shell is Convex, and the Inside Concave.
Term, or Bound, is that which limits any thing; as Points are the Bounds of Lines, Lines the Bounds of Surfaces, and Surfaces the Bounds of Solids.
A Figure is that which is bounded every way.
Figures that be terminated under only one Bound, are Circles, and Ellipses, or Ovals, which are bounded by only one Curve Line.
Figures terminated by several Bounds, or Lines, are the Triangle or Trigon, which hath three Sides and three Angles.
The Square, or Tetragon, which hath four.
The Pentagon, five.
The Hexagon, six.
The Heptagon, seven.
The Octagon, eight.
The Nonagon, nine.
The Decagon, ten.
The Undecagon, eleven.
And the Dodecagon, twelve.
All the aforesaid Figures, and those having a greater Number of Sides: are called by the general Name of Polygon, which signifies Figures having many Angles; and for distinguishing them, there is added the Number of Sides: as a Decagon may be called a Polygon of ten Sides; likewise a Dodecagon is called a Polygon of twelve Sides, and so of others.
Figures, whose Sides and Angles are equal (as those before-named) are called regular Polygons. Those Figures, whose Sides and Angles are unequal, are called Irregular Polygons. Triangles are distinguished by their Sides or their Angles.
As to their Sides; that Triangle which hath its three Sides equal, is called an Equilateral Triangle, and is also equiangular.
That Triangle which hath only two equal Sides, is called an Isosceles Triangle.
And that which hath three unequal Sides, is called a Scalene Triangle.
As to their Angles; a Triangle, which hath one right Angle, is called right-angled; and the Side opposite to the right Angle, is called the Hypothenuse.
That which hath one Angle obtuse, is called an obtuse angled Triangle.
That which hath all the Angles acute, is called an acute angled Triangle.
Quadrilateral Figures, or Figures having four Sides, have different Appellations.
It the opposite Sides are parallel, the quadrilateral Figure is called by the general name of Parallelogram.
If a Parallelogram hath four equal Sides, and the four Angles right ones, it is called a Square.
If all the Sides are not equal, but the four Angles right ones, it is called an oblong, right angled Parallelogram, or simply a Rectangle.
A right Line drawn in a Parallelogram, from one of the Angles to the opposite one, is called a Diagonal; as the Line AB.
If the four Sides be equal, and also the opposite Angles, but not right ones, it is called a Rhombus, or Lozang´.
If two opposite of the four Sides are equal, and the opposite Angles also equal, but not right ones, the quadrilateral Figure is called a Rhomboides.
Also a Square is equiangular and equilateral; an Oblong is equiangular, but not equilateral; a Rhombus is equilateral, but not equiangular: And a Rhomboides is neither equilateral nor equiangular.
Every quadrilateral Figure, that hath neither its Opposite Sides, Parallel, or Equal, is called a Trapezium.
A Circle is a plane Figure, comprehended under one Line, which is called its Circumference, which is equally distant from a Point in the middle, called the Center.
A Semicircle is a Figure terminated by the Diameter and the Semicircumference.
A Portion, or Segment of a Circle, isa Figure comprehended by a part of the Circumference, and a Chord lesser than the Diameter; there is a greater and letter Segment.
A Softer of a Circle is a Figure made by apart of a Circle, terminated by two Radii, or Semidiameters, which do not make a right Line; there is a great and small Sector.
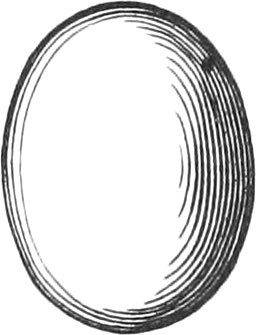
An Ellipsis is a Figure longer than it is broad, comprehended but by one Curve Line, in which the2 two greatest Lines that can be drawn at right Angles to one another, are called the Axes of the Ellipsis; the greatest of which is called the great Axis, and the lesser the least Axis.
The Center of an Ellipsis is that Point wherein the two Axes cut each other.
Those Figures that have the same Center, are called Concentrick Figures.
Excentrick Figures are those that have not the same Center.
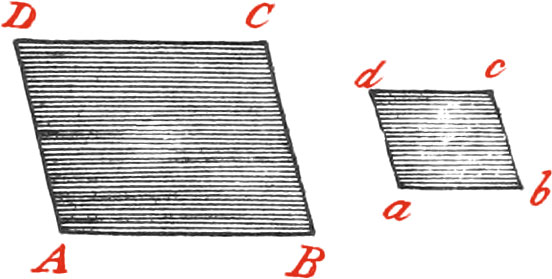
Similar Figures are those which have their Angles equal each to each; that is, which have each Angle of one Figure equal to the correspondent Angle in the other Figure, and have the Sides about the equal Angles proportional. As suppose the Side ab is one half, or one third of the Side AB; then all the other Sides of the lesser Figure abcd, will be likewise one half, or one third of the Sides of the greater Figure ABCD.
The correspondent Sides in this Figure are called homologous Sides; as the Side AB of the greater Figure, and the Side ab of the lesser Figure, are called homologous Sides.
Equal Figures are those that equally contain an equal Number of equal Quantities.
There are Figures that are similar and equal.
Others are equal, and not similar;
And, finally, others are similar, but not equal.
Isoperimetrical Figures are those whose Circuits are equal: As, for Example, the Triangle ABC, and the Square ABCD, are Isoperimetrical Figures; because each Side of the Triangle being 8, its Circuit is 24, and every Side of the Square being 6, its Circuit is also 24 of those equal Parts that make the Circuit of the Triangle.
Body, or a Solid, is that which hath Length, Breadth, and Thickness.
A Sphere, Globe, or Ball, is made by the entire Revolution of a Semicircle about its Diameter, which is at Rest, and which is called the Sphere’s Axis.
A Spheroid is a Solid, made by the entire Revolution of a Semi-Ellipsis about its Axis remaining at Rest.
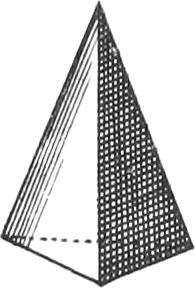
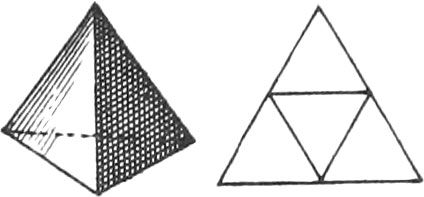
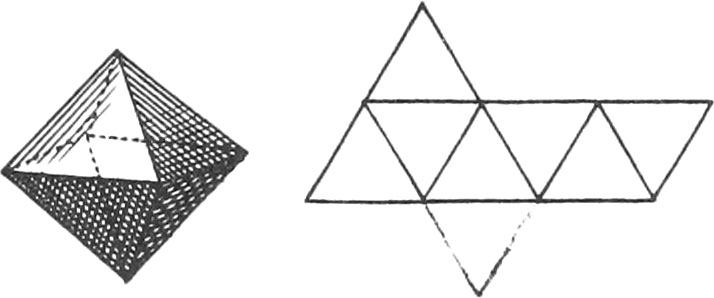
A Pyramid is a Solid contained under Several Triangular Planes meeting in one Point, and having a Polygon for its Base.
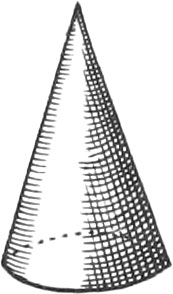
A Cone is a Species of a Pyramid, having a circular Base: This Solid is made by the entire Revolution of a right-angled Triangle about one of the Sides, forming the right Angle, which Side is called the Axis of the Cone.
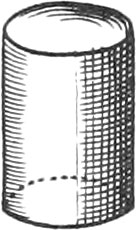
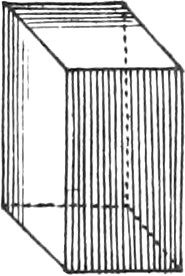
A Cylinder is a Solid, whose Bases are two equal Circles. This Solid is generated by the entire Revolution of a right angled Parallelogram about one of its Sides, which is called the Cylinder’s Axis.
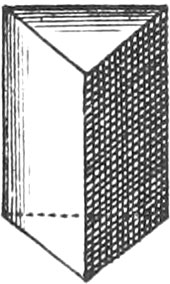
A Prism is a Solid, whose two Bases are two similar, equal, and parallel Planes; and when the parallel Planes are Triangles, the Prism is called a Triangular Prism.
When the two Bases of a Prism are Parallelograms, it is called a Parallelepipedon.
If the Sides of the aforesaid Bodies are perpendicular to the Base, they are called right, or Isosceles Solids.
If they are inclined, they are called Oblique, or Scalenous Solids.
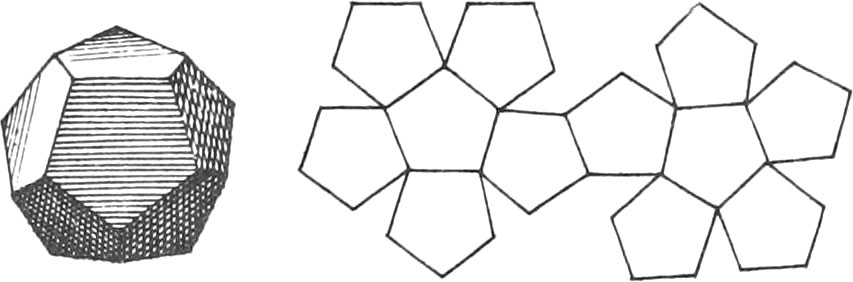
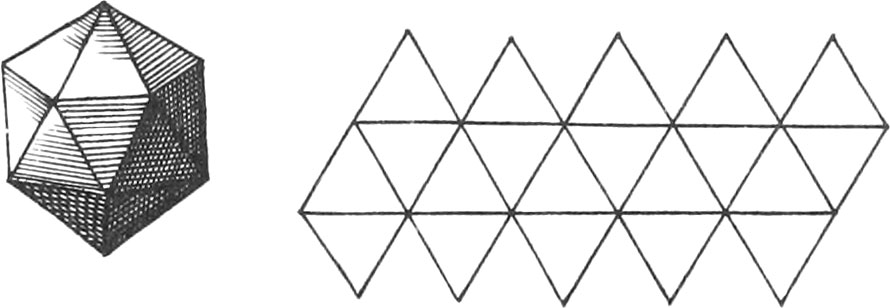
A regular Body is that which is contained under regular and equal Figures, all the solid Angles of which are likewise equal.
A solid Angle is the meeting of several Planes in one Point; as the Point of a Diamond.
There are required more than two Planes to constitute a solid Angle.
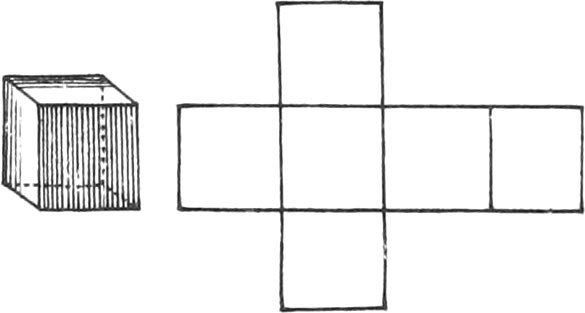
There are five regular Bodies represented in the same Plate, together with the Unfoldings of their Planes, viz.
The Tetrahedron, contained under four equal and equilateral Triangles.
The Hexahedron, or Cube, contained under six equal Squares.
The Octahedron is contained under eight equal and equilateral Triangles.
The Dodecahedron, contained under twelve equilateral and equal Pentagons.
The Icosahedron, contained under twenty equal and equilateral Triangles.
The Unfoldings nigh to each of the aforenamed regular Bodies, shew how to draw them on Brass or Pasteboard, in order to cut them out; which when done, if they are duly folded up, there will be formed the regular Bodies.
All other Solids are called by the general Name of Polyhedron, which Signifies a Body terminated by many Superficies.
If in the following Work, Terms be used that are not here defined, they shall be defined and explained in their proper Places.
- 1Our Author should have said, Lesser Number.
- 2Our Author should have said, the greatest and least Lines. This is not a good Definition of an Ellipsis. See another of mine in the Appendix that I have added.