Book VII. Ch. IV.

Of the Construction and Uses of Mercator’s Charts.

If the Degrees of Latitude are to be augmented as much as those of Longitude are found enlarged by making them equal to the Degrees of the Equinoctial, the Secants must be used, which increase in the same Proportion as the Sine-Complements of the Latitudes (which ought to represent the Degrees of Longitude) have been increased, by making them equal to the Radius of the Equator, because of the Parallelism of the Meridians: for the Sine-Complement of an Arc is to Radius, as Radius is to the Secant of that Arc.

As, assuming for one Degree of the Equator, and for the first Degree of Latitude, the whole Radius, or some aliquot part thereof; take for the 2d Degree of Latitude, the Secant of one Degree, or a similar aliquot part of this Secant; and for the 3d Degree of Latitude, take the Secant of two Degrees, or the similar aliquot part thereof, and so on.

When a Chart is to be made large, you must take, for 30 Minutes of Latitude, and 30 Minutes of the Equator, the Radius of a Circle or some aliquot part thereof, for one Degree of Latitude. This being done, you must add continually the Secant of 30 Min. for 1\(\frac{1}{2}\) Degree of Latitude, the Secant of 1 Degree for 2 Degrees of Latitude, the Secant of 1\(\frac{1}{2}\) Degree for 2\(\frac{1}{2}\) Degrees of Latitude, or their similar aliquot parts; and so proceed on. In doing of which, we use a Scale of equal parts, from which the Secants as they are found in Tables are taken off, by taking away some of the last Figures.

In these Charts the Scale is changed, according as the Latitude is; as, for example, if a Ship fails between the 40th and 50th Parallel of Latitude, the Degrees of the Meridians between those two Parallels will serve for a Scale to measure the Ship’s Way; whence it follows, that there are fewer Leagues on the Parallels, the nearer they are to the Poles, because they are measured by a Magnitude likewise continually increasing from the Equator towards the Poles.

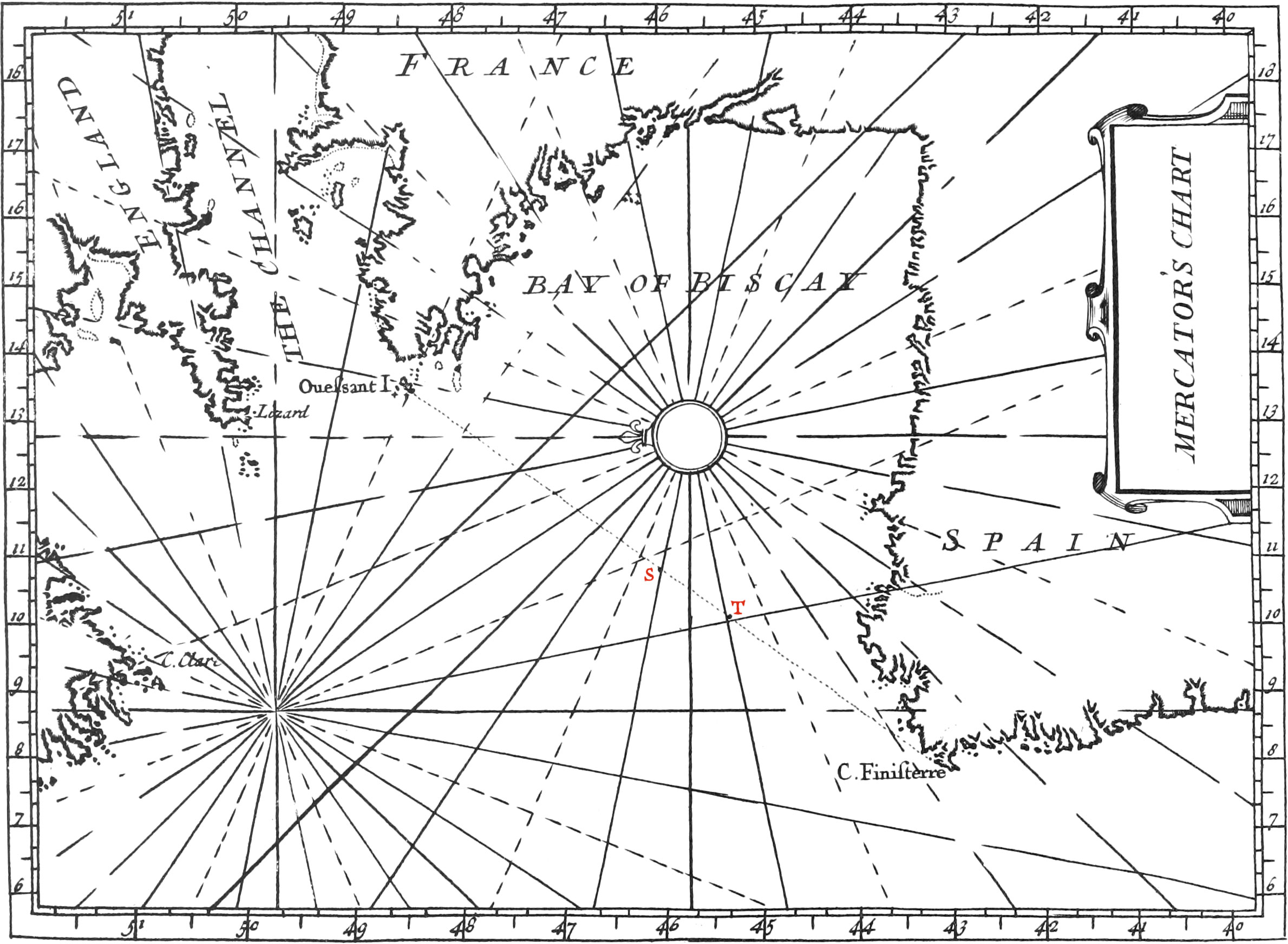
If, for example, a Chart of this kind be to be drawn from the 40th Degree of North Latitude to the 50th, and from the 6th Degree of Longitude to the 18th: First draw the Line AB, representing the 40th Parallel to the Equator, which divide into twelve equal Parts, for the 12 Degrees of Longitude, which the Chart is to contain. Tins being done, take a Sector or Scale, one hundred Parts whereof are equal to each of these Degrees of Longitude, and at the Points A and B raise two Perpendiculars to AB, which will represent two

parallel Meridians, and must be divided by the continual Addition of Secants. As, for the Distance from 40 Deg. to 41 Deg. of Latitude, take 131\(\frac{1}{2}\) equal Parts from your Scale, which is the Secant of 40 Deg. 30 Min. For the Distance from 41 Deg. to 42 Deg. take 133\(\frac{1}{2}\) equal Parts from your Scale, which is the Secant of 41 Deg. 30 Min. For the Distance from 42 Deg. to 43 Deg. take 136, which is the Secant of 42 Deg. 30 Min. and so on to the last Degree of your Chart, which will be 154 equal Parts, viz. the Secant of 49 Deg. 30 Min. and will give the Distance from 49 Deg. of Latitude to 50 Deg. and by this means the Degrees of Latitude will be augmented in the same Proportion as the Degrees of Longitude on the Globe do really decrease.

Having divided the Meridians, you may place the Card upon the Chart, for doing of which, chuse a convenient Place towards the Middle thereof, as the Point R, about which, as a Center, describe a Circle so big that it’s Circumference may be divided into 32 equal Parts, for the 32 Points of the Compass. Then having drawn a Line towards the Top of the Chart, parallel to the two divided Meridians, this will be the North Rhumb, and upon it a Flower-de-Luce must be put, that thereby all the other Rhumbs or Points may be known, the principal of which ought to be distinguished from the others by broader Lines.

After this, all the Towns, Ports, Islands, Coasts, Sands, Rocks, &c. which form the Chart, must be laid down upon the same, according to their true Latitudes and Longitudes. And if the Chart be large, there may several Cards be placed thereon, always with their North and South Lines parallel between themselves.

The use of Mercator’s Charts.

The chief use of a Sea-Chart, is to find the Point of Departure therein, the Point arrived at, the Course, the Distance sailed, the Longitude and the Latitude, as we shall now explain by some Examples.

Example I. Suppose a Ship is to sail from the Island de Ouessant, in 48 Deg. 30 Min. of North Latitude, and 13 Deg. 30 Min. of Longitude, to Cape Finister in Galicia, which is in 43 Deg. of Latitude, and 8 Deg. of Longitude. Now the Point of the Compass the Ship must keep to, as also the Distance between the said two Places is required. In order to do this, you must imagine a Line drawn from the Island de Ouessant to Cape Finister, and with a Pair of Compasses examine what Point on the Chart that Line is parallel to, and this Point, which is South-West, one-fourth South, is that which the Ship must sail on.

But to find the Distance of the two Places, take between your Compasses the Extent of live Degrees on the Meridian against the beforenamed Course, that is, from the 43d Deg. to the 48th; and this will be a Scale of 100 Leagues. This being done, set one Foot of your Compasses thus opened upon the Island de Ouessant, and the other Foot upon the occult Line tending to Cape Finister, making a little Mark thereon; and this Extent of the Compasses will give 100 Leagues of Distance. Then take the Distance from the aforesaid Mark to Cape Finister between your Compasses, and placing one Foot upon the 43d Deg. of the Meridian, and the other Foot will fall upon 44 Deg. 45 Min. which amounts to 35 Leagues; and consequently the whole Distance between Cape Finister and the Island de Ouessant is 135 Leagues.

Example II. A Ship sailing from the Island de Ouessant South-West, one-fourth South, towards Cape Finister, and the Master-Pilot having examined the Force of the Wind, and the Number of Sails spread, and knowing by experience the Swiftness of his Ship, has estimated her Way to have been 50 Leagues in 20 Hours. Now to find the Point upon the Chart wherein the Ship is, he must take the Extent of 2\(\frac{1}{2}\) Degrees, equivalent to 50 Leagues, between his Compasses, upon the Meridian, from the 46th Deg. to the 48\(\frac{1}{2}\) Deg. This being done, if one Foot of the Compasses thus opened be set upon the Place of Departure, the other Foot will fall upon the Point T, the Place wherein the Ship is, on the Line of the Ship’s Way. But if the Longitude and Latitude of the Point T, or Place wherein the Ship is, be sought, he must place one Foot of the Compasses upon the Point T, and the other upon the nearest Parallel, and then conduct the Compasses thus opened perpendicularly along the Parallel to the Meridian and the Degree thereof whereat the Point of the Compasses comes to, will be the Latitude of the Point T. And to find the Longitude of this Point, he must set one Foot of the Compasses therein, and the other upon the nearest Meridian. Then if this Foot be slid along the Meridian (so that a Line joining the two Points be always parallel to itself) to the divided Parallel, he will have, upon that Parallel, the Longitude of the Point T.

Because Meridians and Parallels are not drawn a-cross the Chart, to the end that the Rhumb-Lines may not be confused, therefore you may use a Ruler, which will produce the same Effect.

Example III. The Course being given, and the Latitude by Observation; to find the Distance sailed, and to prick down the Place of the Ship upon the Chart. Suppose a Ship departed from the Island de Ouessant is arrived to a Place whose Latitude, by Observation, is found to be 46 Degrees; take, between your Compasses, the Distance from the 46th Degree of the Meridian to the 48\(\frac{1}{2}\), which is the Latitude of the Place of Departure, over which 48\(\frac{1}{2}\) Degree and the Island de Ouessant having laid a Ruler, slide one Foot of the Compasses thus opened along the Side of this Ruler, ’till the other Foot intersects the Line of the Ship’s Way; then the Point of Intersection S will be that whereat the Ship was at the Time of Observation. Now to find the Distance sailed, you must extend the Compasses from this Point S to the Place of Departure, and lay off this Extent upon the Meridian, which will reach from the 46th Degree to the 49th; and consequently the Distance failed will be 60 Leagues, allowing 20 Leagues to a Degree.

Example IV. The Latitude and Longitude of a Place being given, to find that Place in the Chart. Having placed one Foot of a Sea-Chart Compass upon the known Degree of Latitude, and the other upon the nighest Parallel, you must place with your other Hand one Foot of another Pair of Compasses upon the known Degree of Longitude on the Meridian, and the other Foot upon the nearest Meridian; and then slide both these Pair of Compasses until their two Points meet each other: for then the Point of Concourse will be that sought. This Operation is very much used by Seamen; for the Point where they are, being first found by Calculation, or the Sinecal Quadrant, they can by this means prick down the Place of the Ship upon the Chart, and so it will be easy for them to find what Course the Ship must steer to continue on her Voyage.